Przystanek nauka - portal Uniwesytetu Śląskiego w Katowicach

Autor: dr Jerzy Kuczyński

Pod koniec stycznia (konkretnie w numerze z 21) w Nature ukazał się krótki tekst sugerujący, na podstawie pracy Batygina i Browna (Astr.J. 151 p.22), istnienie nieznanej planety o masie około 10 mas Ziemi. Rzecz ciekawa i na tyle „medialna”, że w zapowiedzi mamy artykuł na ten temat w marcowym numerze Świata Nauki. Wydaje się więc, że nie warto się nad tym zastanawiać – chętnych do tego jest już wystarczająco dużo a rozsądny człowiek tłumu nie lubi. Ale kilkadziesiąt lat temu zlecono mi napisanie seansu na temat X planety. Wówczas ten symbol odczytywano „dziesiąta” bo Pluton był pełnoprawną planetą choć już wówczas były sugestie, że traktowanie Plutona jako planety jest z lekka niepoważne. I właśnie z tego powodu „tak dla sportu” (i wspomnień z młodości gdy próbowałem pisać ów seans) przypomniałem co wiem o tych poszukiwaniach. Otóż początek poszukiwań był dobry. Do „znakomitego” brakuje mu tylko przyzwoitego zachowania pewnych bohaterów. A było tak. Na podstawie perturbacji Urana J. Adams i U. Le Verrier obliczyli orbitę i położenie planety „winnej” tych perturbacji. Adamsowi poszło źle. Ale nie z rachunkami, tylko z prominentnymi astronomami. Konkretnie został zignorowany. Niewiele lepiej poszło Le Verrierowi – został w swoim kraju również zignorowany ( skąd my to znamy - czasem wydaje nam się, że my Polacy jesteśmy oryginalni!). Na szczęście (swoje) miał znajomych za granicą. Poprosił więc J. Galle’a, Niemca pracującego w Berlinie o odpowiednie obserwacje. Już wówczas zrobienie dla znajomego obserwacji, zwłaszcza jeżeli można się dopisać do publikacji, było w modzie. Godzina pracy wraz z studentem (doktorantem) H. d’Arrestem i Neptun był odkryty. Oczywiście potem była rytualna awantura o to kto jest odkrywcą. Pretensje mieli zwłaszcza Anglicy, którzy zignorowali rachunki Adamsa.

W sumie jednak olśniewający sukces (godzina obserwacji wizualnych!). Ale potem było już tylko gorzej. Jeszcze dość nieźle poszło z Plutonem. Kilka lat rachunków i w końcu poszukiwania. C. Tombaugh rozpoczął poszukiwania w 1929 roku i na płycie naświetlonej 18 lutego 1930 roku Pluton został odnaleziony. Tym razem przeszło rok poszukiwań, długotrwałe naświetlania i stosunkowo duża (13 cali) astrokamera. Neptun był około stopnia od przewidywanej pozycji, czyli przy małym powiększeniu można by go zobaczyć na obrzeżach pola widzenia po wycelowaniu teleskopu dokładnie w przewidywaną pozycję. Pluton był 6 stopni od takiej pozycji. Aby znaleźć poszukiwany obiekt trzeba było (jak pisze Tombaugh (S&T April 1991 str 360) około dwu godzin pracy z wytężoną uwagą aby przejrzeć jeden stopień kwadratowy nieba. Trzeba bowiem wiedzieć, że w miejscu gdzie Galaktyka jest najcieńsza na kliszy było 40-60 tysięcy gwiazd. W Strzelcu tam gdzie Galaktyka jest najgrubsza, Tombaugh miał na kliszy przeszło milion gwiazd. Pluton od początku wyglądał podejrzanie i wydawało się, że „właściwa” planeta dopiero czeka na odkrycie. Dlatego poszukiwania trwały jeszcze 15 lat. Przeszukano dziewięćdziesiąt tysięcy stopni kwadratowych znajdując prawie 4000 planetoid połowę mniej gwiazd zmiennych i prawie trzydzieści tysięcy galaktyk. I „I encountered no new planets” konkluduje Tombaugh.

Oczywiście nie powstrzymało to innych. Poszukiwania Tombaugh’a dotyczyły jasności do 16,5 magnitudo. Słabsze obiekty mogły spokojnie kryć się na krańcach Układu Słonecznego. Nietrudno zauważyć, że jasność obiektu w Układzie Słonecznym maleje jak czwarta potęga odległości od Słońca (jeden kwadrat z powodu osłabienia oświetlenia przez Słońce i drugi kwadrat z powodu konieczności powrotu światła odbitego na Ziemię). Dlatego Uran w odległości 200 AU byłby na granicy możliwości Tombaugh’a. A poszukiwana planeta miałaby mieć mniejsze rozmiary i niewielkie albedo. Dlatego poszukiwano głównie obliczeniowo bo próba pracy w stylu Tombaugh’a wydawała się zupełnie nierealna. T. A. Van Flandern i R. Harrington pod koniec lat siedemdziesiątych zasugerowali (wykalkulowali) istnienie planety o masie 3-5 mas Ziemi znajdującej się na dosyć eliptycznej orbicie 50-100 AU od Słońca. Skorzystali ze starej (1934 rok) sugestii A. Lyttletona , że pochodzenie Plutona i Charona (księżyc Plutona) oraz dziwna orbita Trytona (księżyc Neptuna) są z tą planeta związane. Planeta zwana przez Hrringtona „Humphrey” miałaby przechodząc w pobliżu Neptuna porwać dwa z jego księżyców i odwrócić orbitę Trytona. Owe dwa porwane księżyce Neptuna to oczywiście obecny Pluton z Charonem. Rzeczywiście dramatyzmu hipotezie nie brakuje, jednak próby zaobserwowania Humphrey'a nie przyniosły rezultatu. Podobnie nie przyniosły rezultatu (de facto wykluczone przez benedyktyńskie badania Tombaugh’a) poszukiwania planety zaproponowanej przez C. Powella. Miałaby to być stosunkowo niewielka planeta (35% masy Ziemi, na zbliżonej do Plutona orbicie. Ze względu na bliskość do orbity Plutona sugerowaną nazwą była Persefona. Nieco później, bo 1984 roku pojawiła się hipoteza, że Słońce jest gwiazdą podwójną. Owym nieznanym towarzyszem Słońca o nazwie Nemezis miałby być niewielka gwiazda na bardzo wąskiej orbicie (mimośród bliski jeden) zbliżająca się do Słońca raz na 26 milionów lat. Dane obserwacyjne miałyby wynikać z badań paleontologicznych. Wydawało się bowiem (wówczas, może teraz też paleontolodzy tak uważają), że w takim okresie następują na Ziemi wymierania. Podobno inne geologiczne dowody na taką periodyczność też są⁽¹⁾. Mechanizm destrukcyjny jest tu dosyć oczywisty. Nemezis powodowałaby skierowanie do centrum Układu Słonecznego liczne obiekty Obłoku Oorta i Pasa Kuipera, które zderzając się z planetami wewnętrznymi w tym i z Ziemią powodowałyby wspomniane wymierania. Niedługo po modzie na Nemezis J. Anderson zasugerował istnienie planety o masie 5 mas Ziemi na orbicie bardzo silnie nachylonej do ekliptyki. Tym razem „dane obserwacyjne” na podstawie których padła ta sugestia były co najmniej oryginalne. Otóż w XIX wieku planeta miałaby oddziaływać na Urana i Neptuna bo tak wskazują dane z tego okresu. Jednak Pionieer 10 nie podlegał żadnym oddziaływaniom grawitacyjnym, a i współczesne pomiary Plutona nie wskazują na istnienie takiej planety. Wszystko jednak zaczyna się zgadzać jeżeli planeta Andersona była wówczas bardzo blisko tych ciał (m.in. była w pobliżu peryhelium). Obecnie oddaliła się. Następne oddziaływania wg Anderosona około 2600 roku. Oczywiście poszukiwań nie prowadzono. W 1999 roku badania perturbacji orbit komet zasugerowały coś co nazwano Tyche. Tym razem nie gwiazda a brązowy karzeł o dość podobnych do Nemezis własnościach. Ale teraz zbliżamy się do czasów gdy mozolne badania typu tych wykonanych przez Tombaugh’a są już niekonieczne – większość mozolnej pracy z ogromną prędkością wykonują komputery. W 2014 badania w podczerwieni wykluczyły istnienie Nemezis czy Tyche. Tak naprawdę większe ciało, jeżeli miałoby egzystować „na krańcach Układu Słonecznego” to musiałoby być bardzo zimne, czyli być rzeczywiście daleko od Słońca i nie mieć „wewnętrznego źródła ciepła”. Jednak w tym samym roku C. Trujillo i S. Sheppard zaproponowali istnienie dużej planety. No i w końcu bieżące wydarzenia. Batygin i Brown proponują swoją planetę. Twierdzą że prawdopodobieństwo jej istnienia wynika ze „zdumiewającego przypadku”, że kilka obiektów Pasa Kuipera ma bardzo zbliżone peryhelia (a pewnie i inne parametry orbity) wynoszące około 200 AU.

Znana mi historia, już prawie 90 letnich, badań w tej dziedzinie wskazuje, że żadne z tych rachunków się nie potwierdziły. I szybko ulegały zapomnieniu – niedawne przecież doniesienia C. Trujillo i S. Shepparda zacierają mi się już w pamięci – na pewno czytałem tą pracę ale jakie konkretnie dane i rachunki były podstawą do wyciągnięcia wniosków i jakie to były wnioski już nie pamiętam. A biorąc pod uwagę, że jasność planety Batygina i Browna miałaby oscylować w pobliżu 30 magnitudo poszukiwania obserwacyjne wydają się nierealne. Tak więc nawet sugestia „poczekajmy” wydaje mi się mało rozsądna. Chociaż … . Alessandro Morbidelli, bardzo dobry fachowiec od rachunków dynamicznych w Układzie Słonecznym twierdzi, że jest „quite convinced” do istnienia planety „wykalkulowanej” przez Batygina i Browna. Kolega będący doktorantem rachujących dynamiczne układy (gwiazdy wielokrotne), który czytał oryginalną pracę powiedział że „autorzy wyliczyli, że prawdopodobieństwo istnienia takich koincydencji przy braku planety X jest prawie zerowe więc prawdopodobieństwo istnienia planety jest bardzo wielkie”. I to ostatnie mnie przekonało, że … planeta nie istnieje. Warto bowiem się zastanowić nad sensem prawdopodobieństwa. Otóż opisuje ono stan naszej wiedzy, lub jak kto woli niewiedzy. Jest to więc ewidentnie coś zależnego od nas. Można by powiedzieć należącego do naszego świata. Wprawdzie w jakiś sposób prawdopodobieństwo zależy od zewnętrznej rzeczywistości, jednak w pewien sposób jest zawieszone między tymi światami – naszym wewnętrznym i zewnętrzną od nas rzeczywistością⁽²⁾. Jak to w praktyce działa możemy przeanalizować na kilku przykładach. Np. odkrywamy planetoidę NEO (czyli bliską Ziemi). Oczywiście liczymy czy może zderzyć się z Ziemią. Jednak pomiar położenia planetoidy został dokonany z pewną dokładnością. Podobnie z czasem. Dlatego im dalej od momentu pomiaru tym mniej dokładnie znamy położenie i moment w którym to położenie zostanie osiągnięte. Jeżeli obszar niepewności (w czasoprzestrzeni bo w tym przypadku liczy się i czas i przestrzeń) obliczenia orbity planetoidy i położenia Ziemi ma część wspólną to mówimy, że zderzenie jest prawdopodobne. Oczywiście im większa jest wspólna objętość przestrzeni którą jednocześnie zajmuje planetoida i Ziemia tym prawdopodobieństwo zderzenia większe. Widać jednak że zależy to od naszej wiedzy. Im lepiej określona orbita planetoidy (oraz Ziemi) tym nasza wiedza bliższa pewności, czyli prawdopodobieństwo lepiej określone (z większym przekonaniem wiemy czy zderzy się czy nie). Nietrudno zauważyć, że odpowiednio do wzrostu naszej wiedzy prawdopodobieństwo się zmienia. Przy czym wzrost wiedzy może zarówno zwiększać jak i zmniejszać prawdopodobieństwo jakiegoś wydarzenia (p. Rys 1). Co więc określa prawdopodobieństwo? W pierwszym rzędzie określa je tzw. przestrzeń zdarzeń, czyli mówiąc prosto co uważamy, że może się zdarzyć. I najistotniejsza jest tu fraza „co uważamy”. Jeżeli nasze uważanie dobrze zgadza się z rzeczywistością to i obliczone prawdopodobieństwo odpowiada rzeczywistości czyli zdarzenia o dużym prawdopodobieństwie zdarzają się często a zdarzenia o małym prawdopodobieństwie rzadko. Można więc prawdopodobieństwo po prostu zmierzyć. I owszem można, ale pod warunkiem, że zdarzenie ma charakter powtarzalny a przynajmniej zdarza się dosyć często. Wówczas można je zmierzyć uznając, że prawdopodobieństwo to po prostu ilość zdarzeń na jakiś przedział parametru (np. liczba zdarzeń na ilość gier czy przedział parametru). Jednak często, żeby nie powiedzieć „w praktyce zawsze” interesuje nas prawdopodobieństwo zdarzeń zachodzących rzadko czy wręcz z definicji zachodzących jednorazowo, tak jak zderzenie planetoidy z Ziemią. Po prostu w praktyce życiowej, a w naukowej wcale nie jest inaczej, interesuje nas głównie czy coś się uda lub nie. Tak jak to jest z opisywanym na Rys.1 przypadkiem czy planetoida zderzy się z nami czy nie. Podobnie jest i w przypadku planety na krańcach Układu Słonecznego – jakie jest prawdopodobieństwo, że istnieje? Aby to ocenić budujemy przestrzeń zdarzeń czyli mówiąc prosto wyobrażamy sobie wszystkie możliwe wydarzenia a następnie obliczamy jaka część wszystkich zdarzeń prowadzi do interesującego nas skutku. Stosunek tych interesujących do całości jest prawdopodobieństwem. Warto zauważyć, że zwykle gdy już wyobrazimy sobie wszystkie możliwości to ilość możliwości sprzyjających danemu wydarzeniu udaje się zwykle obliczyć standardowymi metodami. W dużej mierze obliczanie prawdopodobieństw w powyższym sensie sprowadza się więc do dobrej wyobraźni. A z tą u ludzi zwykle kiepsko. Dlatego poleganie na „wyrachowanych” prawdopodobieństwach często prowadzi do do nieprzyjemnych skutków. Przykładem może służyć sprawa szyfrów – ich twórcy obliczają „prawdopodobieństwo” ich złamania jako zupełnie zaniedbywalne, z zasady dlatego że według nich przestrzeń zdarzeń jest bardzo wielka. A jednak często okazuje się, że z jakichś powodów ta przestrzeń jest w rzeczywistości dużo mniejsza i odpowiednio do tego zmniejszenia objętości przestrzeni zdarzeń szyfr udaje się złamać. Szczególnie drastycznie wygląda to gdy prawdopodobieństwa używa się jako dowodu sądowego. Czytałem (bodaj Delta) o przypadku gdy kobiecie zmarło dziecko. Po prostu zmarło w łóżeczku. Medycyna zna takie przypadki. Niestety kilka lat później rzecz się powtórzyła (oczywiście z innym dzieckiem). Pojawiło się więc podejrzenie dzieciobójstwa. Biegły sądowy obliczył bardzo niewielkie prawdopodobieństwo, że zdarzą się dwa takie przypadki w jednej rodzinie. Nic dziwnego – samo zdarzenie jest mało prawdopodobne a prawdopodobieńst6wo, że zdarzy się to w jednej rodzinie biegły obliczył jako kwadrat tej i tak niewielkiej liczby. Na podstawie tego rachunku kobietę skazano. Po długich i kosztownych badaniach udało się wykazać, że w rodzinie występuje rzadkie schorzenie powodujące takie właśnie skutki (śmierć w łóżeczku). Kobietę udało się więc uniewinnić (p. Rys 2). Niestety pewnych nieodwracalnych skutków procesu już odwrócić się nie dało – wypuszczona z więzienia kobieta była już nieodwracalnie chora psychicznie – nic specjalnie dziwnego śmierć dwójki dzieci proces i odsiadka to dla przeciętnego człowieka trochę dużo. A biegły w roli kary otrzymał „roczny zakaz pełnienia funkcji biegłego”.

Tak w ogóle to wydaje się, że mało prawdopodobne wydarzenia są same w sobie interesujące i można skonstruować całą ich hierarchię. Na początek, warto zauważyć, że prawdopodobieństwo równe zero nie oznacza zdarzenia niemożliwego. W pewnym sensie większość zdarzeń zachodzących w realnym świecie charakteryzuje się takim prawdopodobieństwem – wyemitowanie przez atom fotonu w dokładnie określonym kierunku ma prawdopodobieństwo równe zero. A jednak w jakimś kierunku foton wzbudzonego atomu leci. Podobnie prawdopodobieństwo trafienia w konkretny punkt przy losowym rzucie „punktu” na jakiś obszar też jest równe zero. I znowu w jakieś miejsce rzucony punkt upadnie. Tym samym nie są to zdarzenia niemożliwe. Jeden z moich Kolegów podaje studentom jako przykład zdarzenia niemożliwego wyjechanie windą na szóste piętro w budynku pięciopiętrowym. Mówiąc bardziej formalnie niemożliwym jest zdarzenie spoza przestrzeni zdarzeń. Ale problem zderzenia planetoidy z Ziemią i „śmierci łóżeczkowej” jasno pokazuje, że przestrzeń zdarzeń za niezmienną może uważać matematyk (którym jest wspomniany Kolega). Z praktycznego (fizycznego) punktu widzenia przestrzeń zdarzeń jest zmienna i zależy od każdego nowego pomiaru czy hipotezy. Można więc spróbować wymyślić „hierarchię niemożliwości”. Niewątpliwie umiarkowanie niemożliwe jest zdarzenie tak „w ogóle możliwe” ale leżące poza przestrzenią zdarzeń. Powiedzmy zderzenie planetoidy z Ziemią gdy z kalkulacji wynika, że planetoida minie Ziemię. Wystarczy jakiś zignorowany mechanizm np. „zielone ludziki”⁽³⁾. W przykładzie z domem byłoby to wyjechanie windą na pierwsze piętro w domu gdzie winda zatrzymuje się od drugiego piętra. Nieco bardziej niemożliwe jest wydarzenie podawane przez kolegę. Szóstego piętra nie ma. Ale oczywiście można go dobudować. Czy może być coś bardziej niemożliwego? Oczywiście , np. wylosowanie trójkąta o trzech kątach prostych albo koła o średnicy równej obwodowi. Chwileczkę, a geometria sferyczna? A przestrzeń w pobliżu czarnej dziury? I w tym momencie widzimy, że tak naprawdę ograniczeniem jest jedynie nasza wyobraźnia i … rzeczywistość fizyczna⁽⁴⁾. Nie warto chyba dalej ciągnąc tych rozważań i lepiej wrócić do problemu istnienia planety X. I tu sprawa jest oczywista. Pomijając ocenę praktyczną („Widziałem wiele takich propozycji w swojej karierze. I wszystkie okazały się błędne” Hal Levison wspomniany na początku 529 tom Nature str.266) warto popatrzeć na Rys.3. Widać że wystarczy „zgubić” jeden parametr by prawdopodobieństwo okazało się drastycznie mniejsze od wyliczonego. I jestem skłonny sądzić że taka sytuacja ma miejsce w przypadku większości ocen prawdopodobieństwa których nie można zweryfikować przez wielokrotne powtarzanie⁽⁵⁾.

⁽¹⁾ Są i inne hipotezy dotyczące przyczyn takiej periodyczności. Jedną z nich jest oscylacyjny ruch Słońca w osi prostopadłej do płaszczyzny Mlecznej Drogi – co taki okres Słońce miałoby przechodzić przez płaszczyznę galaktyki i tam znajdować się pod wpływem … . Nie pamiętam już jakie to czynniki miałyby wówczas destruktywnie wpływać na naszą planetę.

⁽²⁾Nie jest to nic specjalnie dziwnego. Cała nasza wiedza przyrodnicza zawiera „składową ludzką”. Wydaje się, że nie jest możliwe stworzenie nauki nie zawierającej takiej składowej. Byłaby w pewnym sensie nauka tożsama z samą rzeczywistością. Jednak z zasady staramy się te składowe odróżniać. Typowym sposobem są cechowania. Najczęściej budujemy teorię a następnie badamy czy nie jest ona zależna w jakimś stopniu od naszej woli. Określenie sposobu w jaki teoria jest „wolozależna” traktujemy jako symetrię i za „istotnie fizyczną” uważamy klasę równoważności względem tej symetrii. Przykładem może być zależność mechaniki klasycznej od wyboru układu współrzędnych czy układu jednostek, a nieco bardziej abstrakcyjne od transformacji kanonicznych, które to zależności traktujemy jako symetrie i za „istotnie fizyczne” uważamy wielkości które od tych symetrii nie zależą. Dlatego fakt, że prawdopodobieństwo nie jest w pełni fizyczne nie powinien budzić zdziwienia.

⁽³⁾Zielone ludziki mogą bardzo silnie wpływać na rzeczywistość. Dlatego jestem przeciwnikiem, bardzo bezpiecznej w normalnej przestrzeni zdarzeń, energetyki jądrowej.

⁽⁴⁾ A więc moja klasyfikacja zdarzeń niemożliwych byłaby taka:

1. Zdarzenia leżące w przestrzeni zdarzeń ale o prawdopodobieństwie równym zero.
2. Zdarzenia spoza przestrzeni zdarzeń ale tak w ogóle gdzieś egzystujące (egzystują jego realne elementy), tak że przy odpowiednim powiększeniu przestrzeni zdarzeń zostaną w niej zawarte.
3. Zdarzenia spoza przestrzeni zdarzeń, których realne elementy nie istnieją ale które można skonstruować.
4. Zdarzenia spoza przestrzeni zdarzeń, których konstrukcja wydaje się z zasadniczych powodów niemożliwa.

W pewien sposób powyższa hierarchia prawdopodobieństw jest hierarchią istnienia – im wyższy numer w tej klasyfikacji tym bardziej wg mnie zdarzenie nie istnieje. Zapewne powyższa klasyfikacja ma spore wady ale w praktyce jest przydatna umożliwiając praktyczną ocenę realności zdarzeń.

⁽⁵⁾ Pojawia się bardzo interesujący problem czy prawdopodobieństwo nie związanie z wielokrotnie powtarzanymi zjawiskami może mieć „obiektywny sens fizyczny” czy też jest jedynie miarą naszej wiedzy i niewiedzy. Można wyobrazić sobie, że ma taki sens. Nie potrafię jednak wymyślić fizycznej realizacji takiego przypadku nie związanego z wcześniejszym wielokrotnym powtórzeniem lub rachunkiem przez istotę myśląca. W tym ostatnim przypadku rzecz jest dosyć prosta i realizują to gry hazardowe. - po wcześniejszym przeliczeniu (i sprawdzeniu eksperymentalnym że model jest dobry) można ustalić wygrane w grach liczbowych tak by wypłata dzięki realnemu istnieniu prawdopodobieństwa powodowała stałe zyski dla właściciela kasyna. Przy okazji przypomina mi się opowiadanie bodaj J. Londona o człowieku, który co wieczór przychodził do kasyna i inkasował określoną sumę. I w tym przypadku był to problem przestrzeni zdarzeń. Rzecz działa się na Alasce i ruletka stała przy rozgrzanym piecu co spowodowało wypatrzenie mechanizmu dzięki czemu pewne liczby wypadały częściej.

Rysunki:

Rys.1.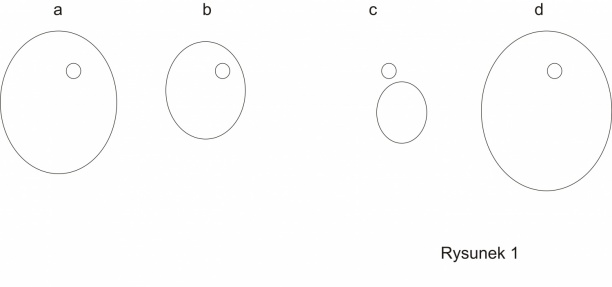

Większe koło przedstawia niepewność określenia położenia NEO . Małe kółko to położenie Ziemi. Dla uproszczenia przedstawiono to na płaszczyźnie. W rzeczywistości wszystko zachodzi w przestrzeni trójwymiarowej i czasie – zderzenie nastąpi wówczas gdy NEO i Ziemia znajdą się jednocześnie w tym samym punkcie. Poza tym w celu wyliczenia prawdopodobieństwa trzeba uwzględnić, że nie wszystkie punkty i momenty czasu są równo prawdopodobne (ta sama objętość czasoprzestrzenna na brzegu „obszaru niepewności” odpowiada innemu prawdopodobieństwu niż w pobliżu jego centrum), ale „ideologia” jest taka jak przedstawia poniższa sekwencja.

• a. Obszar niepewności położenia NEO ma część wspólną z położeniem Ziemi. Zderzenie jest prawdopodobne.
• b. W wyniku poprawy pomiarów i obliczeń orbity NEO obszar niepewności się zmniejszył i dalej obejmuje położenie Ziemi. Prawdopodobieństwo zderzenia wzrosło.
• c. W wyniku dalszych obserwacji i odpowiednich rachunków poprawiono dokładność orbity NEO i obszar niepewności nie ma części wspólnej z Ziemią – prawdopodobieństwo zderzenia wynosi zero.
• d. Zauważono, że poprzednie rachunki nie uwzględniały jakiegoś czynnika, np. odkryto, że NEO wykazuje aktywność kometarną (wydzielanie gazów) zmieniającą nieco orbitę tak, że znowu prawdopodobieństwo zderzenia jest niezerowe!

Rys.2.

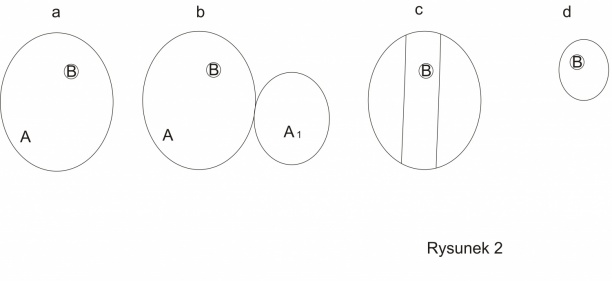
Prawdopodobieństwo obliczamy jako stosunek miary obszaru zdarzeń sprzyjających danemu wydarzeniu do miary obszaru odpowiadających wszystkim możliwym wydarzeniom czyli przestrzeni zdarzeń . Przy czym dla „uproszczenia” miarę przestrzeni zdarzeń normujemy do jedności.

• a. Prawdopodobieństwo wydarzenia B jest ilorazem miary obszaru B i miary obszaru A.
• b. Jeżeli z jakichś powodów trzeba powiększyć przestrzeń zdarzeń o obszar A' to oczywiście prawdopodobieństwo B maleje. Oczywistym powodem powiększania przestrzeni zdarzeń jest zauważenie dotychczas niebranych pod uwagę zdarzeń.
• c. W wyniku badań może okazać się że przestrzeń zdarzeń należy zmniejszyć. Np. poprzez dokładniejsze rachunki czy pomiary udaje się wykluczyć pewne zjawisko. Wówczas prawdopodobieństwo rośnie.
• d. Podobną dyskusję można przeprowadzić w stosunku do obszaru zdarzeń sprzyjających”. Omawiana „śmieć łóżeczkowa” stanowi taki przypadek- dodatkowy czynnik (choroba genetyczna) może spowodować, że zdarzenie okazuje się dużo bardziej prawdopodobne niż się to dotychczas wydawało – w przestrzeni zdarzeń rozważanych przypadków (śmierci łóżeczkowych) większość obszaru zajmują zdarzenia związane z daną chorobą. De facto zmienił się obszar zarówno przestrzeni zdarzeń jak i obszar zajmowany przez „zdarzenia sprzyjające”.

Rys.3.

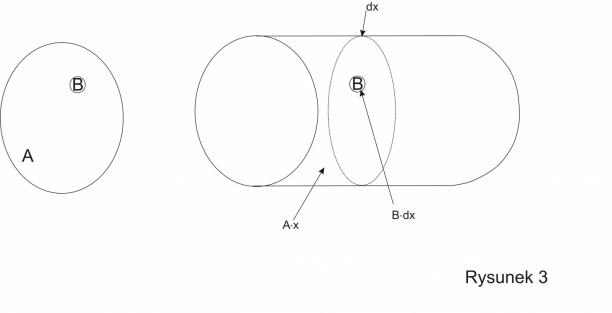
Typowym przypadkiem jest odkrycie nowego parametru od którego zależą zdarzenia. Jeżeli „zdarzenia sprzyjające” odpowiadają wąskiemu zakresowi tego parametru to przestrzeń zdarzeń gwałtownie rośnie a obszar sprzyjający rośnie umiarkowanie. W sumie prawdopodobieństwo maleje prawie do zera.

• a. Pierwotna przestrzeń zdarzeń i obszar sprzyjający.
• b. Po „odkryciu parametru x” jeżeli zdarzeniu sprzyja jego fragment dx to nowe prawdopodobieństwo jest opisane wzorem m(B^.dx)/m(A^.x), gdzie m oznacza miarę obszaru. Prawdopodobieństwo zmalało zgodnie z czynnikiem dx/x.