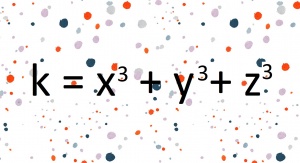Matematyczna zagadka Diofantosa - prawie - rozwiązana
Matematyk z Uniwersytetu w Bristolu znalazł rozwiązanie dla ponad 60-letniej zagadki matematycznej – jak otrzymać liczbę 33 z równania zawierającego sumę sześcianów trzech liczb całkowitych.
Diofantos, starożytny myśliciel, uwielbiał zagadki matematyczne. Niektóre z nich do dziś przedstawia się jako łamigłówki do rozwiązywania na różnych etapach kształcenia. Pamiętając o pasji tego filozofa, matematycy nazwali jego imieniem typ równań, których rozwiązań szuka się w zbiorze liczb całkowitych i naturalnych. W śród takich równań pojawiło się jedno, które stało się podstawą dylematu w zakresie teorii liczb, nad którego rozwiązaniem matematycy głowią się już od 1950 roku. Oto on:
k = x3 + y3 + z3
Czy dla każdej całkowitej liczby „k” da się stworzyć równanie, w którym suma sześcianów trzech liczby całkowitych jest równa tej liczbie?
Przez długie lata odpowiedź na ten dylemat nie była znana. Wraz ze wzrostem mocy obliczeniowych komputerów udało się ustalić rozwiązanie dla większości liczy całkowitych w przedziale od 1 do 100, a dodatkowo dowiedziono, że rozwiązanie nie jest możliwe dla tych liczb, które dzielone przez 9 pozostawiają resztę 4 lub 5 (na przykład 67/9 to 7 i 4 reszty, ponieważ 7*9 + 4 = 63 + 4 = 67).
Do niedawna jeszcze dwie liczby spędzały sen z powiek matematyków, ponieważ nie udało się ani zaproponować ani wykluczyć równania odpowiedniego dla nich. Te liczby to 33 i 42. Dzięki wytężonej, kilkutygodniowej pracy komputerów dr. Andrew Bookera ze Szkoły Matematyki Uniwersytetu w Bristolu, teraz pozostało już tylko 42.
Rozwiązanie dla liczby 33, cóż, nie wygląda na intuicyjne:
33 = (8,866,128,975,287,528)³ + (–8,778,405,442,862,239)³ + (–2,736,111,468,807,040)³
Odpowiedź była możliwa dzięki pracy procesorów, które po prostu przeglądały kolejne możliwe odpowiedzi. To oznacza, że nadal nie mamy systemowej odpowiedzi w postaci algorytmu. Tymczasem dr Booker pracuje obecnie z matematykami z MIT nad ustaleniem równania dla liczby 42.